Surveys and questionnaires are fairly common today, and I believe most people must have filled out a few before. When I fill out questionnaires, I often cannot help thinking if the designer has tried to fill out his/her own questionnaire (eating your own dog food), because some questions are essentially very difficult to answer, although they look easy.
Earlier last month, I took the 2018 Stack Overflow Developer Survey, and I found a few really difficult questions, such as the one that asked me to rank 10 aspects of a job opportunity in order of importance:
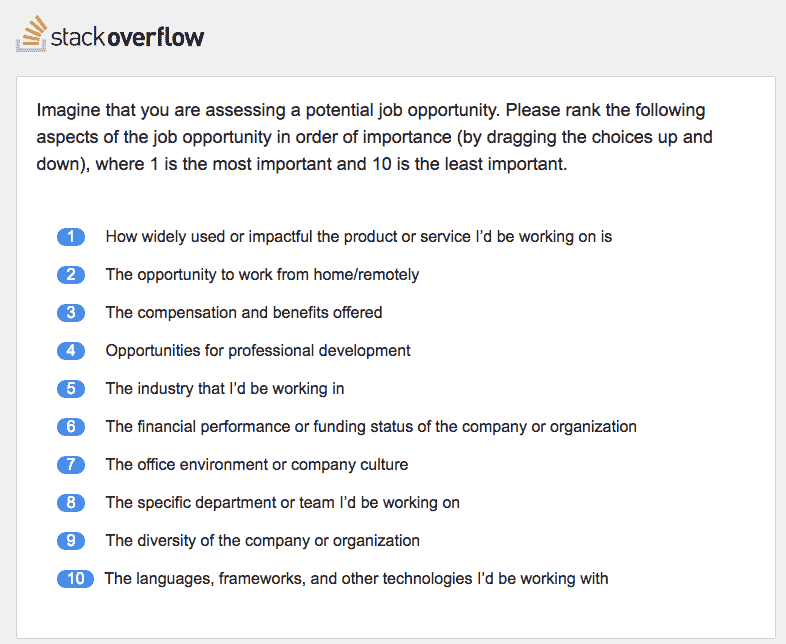
You may think 10 is a small number. Indeed it is. I can count to 10 without using my toes. The problem is that when you compare n aspects with each other, you will end up with doing n * (n + 1) / 2 comparisons. In this case, you need to do 55 comparisons to accurately answer this question. How long do you think it will need to make 55 decisions? The time is probably not trivial. Also consider that this is only one of the many questions in the survey.
So what would a busy developer do? For me, I just dragged the most important aspect to the top, and left the rest of them untouched. I could imagine some other people would do the same. If any Stack Overflow employee (hey Julia) is interested, it will be great to verify it next year: randomize the 10 options for every developer who is going to fill out the questionnaire, and check if only a very small number of options have been moved when the survey is done. It could be verified this year, but since everyone filled out the same questionnaire, there is a tiny probability that most people actually agreed the default order was the order they believed to be appropriate. Without randomization, it is hard to exclude this possibility.
BTW, I’m not really sure how I should interpret the results of such surveys when they are published, because they are based on convenience sampling. For example, developers of one programming language could be more responsive than those of another language, so it could be potentially biased to infer that one language is more popular than the other.