Cohen’s d

蔡锐（真 · 师弟）在审稿时碰到一个新术语，Cohen’s d。他母鸡这是个什么东东；作为名牌大学的统计系博士生，他问了身边的其他博士生，也没什么人知道。我感觉这件事说明两个可能性（至于哪个可能性更大，我不知道）：

1. 这概念压根儿没什么卵用；

2. 现今的统计博士生研究的东西太专了；

在下不才，早年间因为跟心理学研究者打交道的关系，对这个概念略有耳闻，但如今也忘了它的定义，于是再翻了一下维基百科。它就是两样本均值之差除以（合并的）标准差。看起来与 t 统计量类似，区别只是后者除的是标准误，差一个样本量的平方根。

这都不是我想说的重点。重点是维基百科页面上那个该死的用来说明 d 的大小的表格，比如 d 为 0.01 表示“非常小”，d 为 0.2 表示“小”，等等。我觉得这种看起来像权威指导原则的表格一方面是一种统计方法入侵其它学科的最佳工具，另一方面也是它作茧自缚的开端。看看 P 值的下场就知道：很多人大概只记住了一样东西，就是 0.05，至于为什么是 0.05 以及是谁脑子一抽抽想出来的 0.05，管那么多干啥。Cohen’s d 没有像 P 值一样被广大群众吐槽，只不过是它没广泛流行起来罢了（跟胡林翼死太早是一个道理）。

那吃瓜群众可能要起哄了：你行你上啊！

我觉着吧，何必定死那几个数字呢。给几幅图，d 是大是小，应用者自己看着办。比如在配对 t 检验中，我们完全可以给出与特定 d 值对应的概率（五条虚线标出的是维基页面上那个表格里的数字）：

n = 30  # 样本量（只是一个例子）
x = seq(0, 12, 0.01)
par(mar = c(4, 4, 0.2, 0.1))
plot(x/sqrt(n), 2 * (1 - pt(x, n - 1)), xlab = "d = t / sqrt(n)", type = "l", panel.first = grid())
abline(v = c(0.01, 0.2, 0.5, 0.8, 1.2, 2), lty = 2)

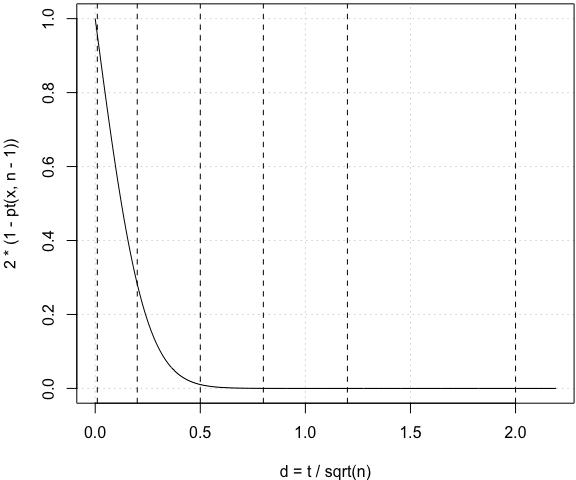
这条线会随着样本量不同而左右收放。我觉得这样一幅笑而不语的图比那个看起来神圣的表格客观得多，但显然，不会有人愿意看这幅图的，因为需要动脑子啊：比如万一碰上个概率 0.057 神马的，它到底算大还是小呢，好纠结哦；无法引用 Cohen 和 Sawilowsky 大人指定的标准，万一审稿人质疑起来，心里会好怕怕。