我翻了一下,上一次写跟统计有关的话题已经是2010年的事情了,多数时候,这里写的都是(计算机)技术类与生活类的话题,于是我又想起来很久以前有客官说,你还不如改成“Keep on eating”算了。废话少说,言归正传。
最近有客官问:
在分段线性回归中,转折点的连续性是必须的吗?
意思是这样,下图中,两段直线应该接着呢(实线),还是可以各走各的(虚线)?
set.seed(123)
# 真实模型
x = sort(runif(100))
y = 2 + 1 * x + 4 * (x > 0.5) + 3 * (x - 0.5) * (x > 0.5) + rnorm(100)
par(mar = c(4, 4, 0, 0), family = "serif", mgp = c(2, 1, 0))
plot(x, y, pch = 20, col = "darkgray")
# 斜率不同,截距限制
fit1 = lm(y ~ 1 + x + I((x - 0.5) * (x > 0.5)))
lines(x, fitted(fit1), lwd = 2, col = 2)
# 斜率不同,截距也不同
fit2 = lm(y ~ 1 + x + I(x > 0.5) + I((x - 0.5) * (x > 0.5)))
lines(x, fitted(fit2), lwd = 2, lty = 2)
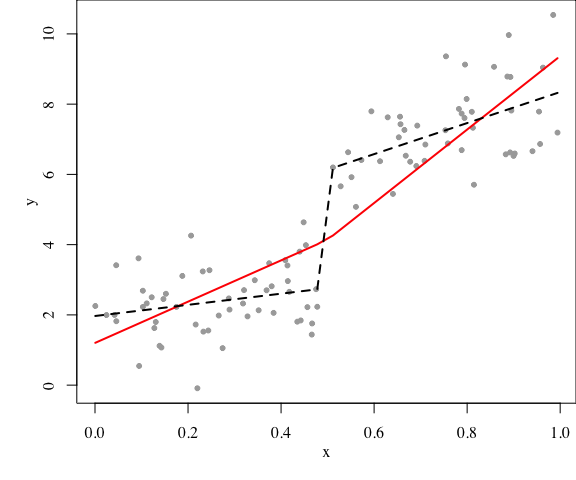
虚线线段的中间一段不应该被画出来,我偷了个懒画上去了,本来应该是间断的。连与不连,归根结底,只不过是回归设计阵要不要多一列的问题。这是线性回归中经典的模型比较问题,上面fit2是全模型,fit1是取消一个限制的模型,自由度之差为1,残差平方和之差除以1,再除以全模型的残差平方和除以相应自由度(88/96),就是F统计量,P值也就出来了。R里面所谓的anova()函数,就是干这事儿的:
# 两个嵌套模型做F检验
anova(fit1, fit2)
## Analysis of Variance Table
##
## Model 1: y ~ 1 + x + I((x - 0.5) * (x > 0.5))
## Model 2: y ~ 1 + x + I(x > 0.5) + I((x - 0.5) * (x > 0.5))
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 97 155
## 2 96 88 1 66.6 72.6 2.2e-13 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
这里因为我们设计的真实模型就是两部分直线斜率和截距在0.5前后都不同,所以这里F检验高度显著,说明加上截距限制条件不合理。道理很简单:除非简约模型和全模型没有显著差异,我们只能认为全模型相对“好”一些。
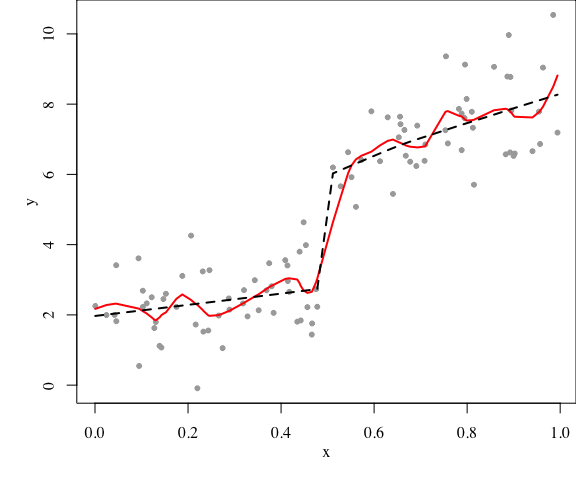
然而,线性模型本身就是对现实的简化。按照上面的想法,其实我们还需要看更复杂的全模型,否则不能认为线性模型就是合适的模型,比如可以考虑非线性模型。复杂模型是没有尽头的,如果要一个个检查下去,那大家都不用干活了。2008年我在COS写了一篇简单的LOWESS文章,如今我仍然可以把它搬出来,因为LOWESS实在是回归模型中的战斗机,它是模型复杂与简约的很好平衡。前面的直线回归可以看作LOWESS的特例,如下fit4。我们可以构造一个相对复杂的LOWESS模型(span参数取小一些),然后和一个简单的模型比较,如:
fit3 = loess(y ~ x, span = 0.2)
fit4 = loess(y ~ 1 + x + I(x > 0.5) + I((x - 0.5) * (x > 0.5)), span = 1, degree = 1)
par(mar = c(4, 4, 0, 0), family = "serif", mgp = c(2, 1, 0))
plot(x, y, pch = 20, col = "darkgray")
lines(x, fitted(fit3), lwd = 2, col = 2)
lines(x, fitted(fit4), lwd = 2, lty = 2)
anova(fit3, fit4)
## Model 1: loess(formula = y ~ x, span = 0.2)
## Model 2: loess(formula = y ~ 1 + x + I(x > 0.5) + I((x - 0.5) * (x > 0.5)), span = 1, degree = 1)
##
## Analysis of Variance: denominator df 82.38
##
## ENP RSS F-value Pr(>F)
## [1,] 15.16 83.2
## [2,] 4.02 87.7 0.321 0.99
P值很大,这毫不奇怪,因为真实模型就是按照两段直线构造的。弯弯曲曲的复杂模型无法打败简单模型,此时我们可以有点底气说两个线段的直线回归可能是对数据的一个恰当描述。
客官的第二个问题是:
转折点怎么确定?
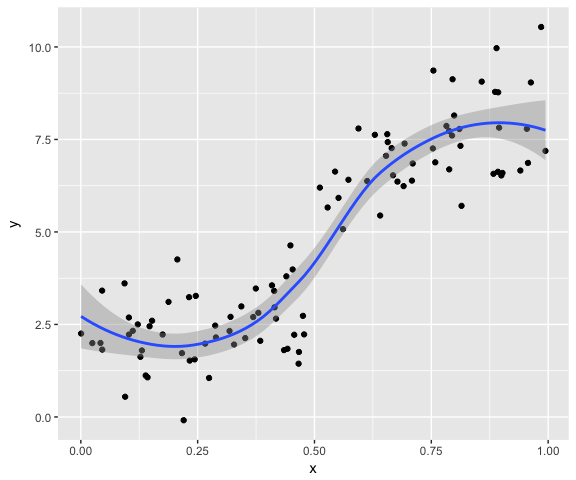
好问题。我对学术研究其实没多大兴趣,所以懒得去文献堆里翻找。我总觉得很多研究是把问题复杂化了,这种文献海让我觉得窒息。如果是我,第一步肯定是画平滑曲线,然后再去结合具体事件背景去决定。如前面的数据用ggplot2很容易分组画图:
library(ggplot2)
qplot(x, y) + geom_smooth() # 总趋势
qplot(x, y, group = x > 0.5) + geom_smooth() # 按0.5前后分组
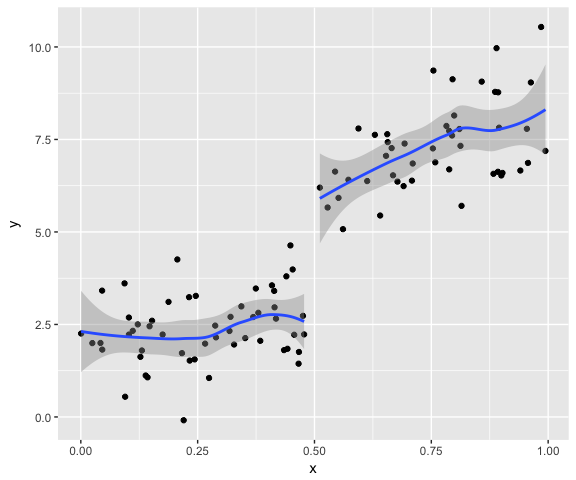
显然所有数据放一条线上建模不合适。作为普通青年的我,到此就止步了(所以我离学术还十万八千里)。不过作为二青年想起一件事,如果不知道转折点,而靠不断推移转折点、新建模型、比较模型得来的转折点,是否有多重比较的嫌疑?比如先试0.2为转折点,再试0.3,……,一直试到0.9,看哪个模型跟全模型比起来没有显著差异。或者说,如果本来真实模型中不存在这样一个转折点,而通过这种方法找出转折点的概率有多大?我估计我八成问了一个很二的问题,应该早有人研究过了。做个模拟应该也不难。
本文是我第一次在博客里尝试 knitr 包,点击页面底部的编辑链接查看源文件(需要 GitHub 账户)。关于 knitr,待我下回在COS详细分解(预览);昨天刚提交 0.5 版本到 CRAN,最终实现了我的初步理想:会 R 就会动态生成报告,把 LaTeX 扔一边儿去吧!