t检验方差不齐有多重要

传统统计教科书大多会提及t检验中方差齐性这个问题，因为检验的假设条件是需要总体方差相等的。然而这个问题实际上可能并没有人们想象的那么重要，这里给两个简单的数值计算结果，看看方差不等对检验结果有什么影响。

par(mar = c(4, 4, 0.5, 0.5), mfrow = c(1, 2))
set.seed(123)
plot(pval <- t(replicate(1000, {
    x1 = rnorm(100, mean = 0, sd = runif(1, 0.5, 1))
    x2 = rnorm(100, mean = 1, sd = runif(1, 2, 5))
    c(t.test(x1, x2, var.equal = TRUE)$p.value, t.test(x1, x2,
        var.equal = FALSE)$p.value)
})), xlab = "P-value: equal variance", ylab = "P-value: unequal variance",
    pch = 20, asp = 1)
abline(0, 1)
plot(pval[, 1], pval[, 2] - pval[, 1], xlab = "P-value: equal variance",
    ylab = "Diff of p-values (unequal var - equal var)", pch = 20)

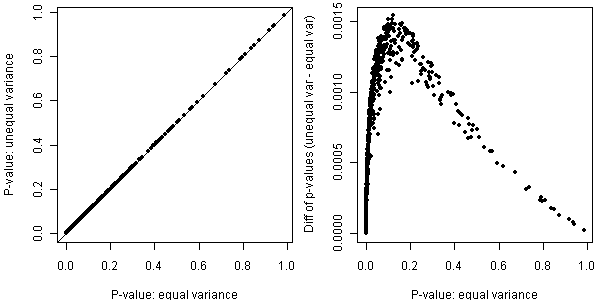
过程是：从两个正态总体中生成样本，第一个总体均值为0，标准差随机取自U(0.5, 1)，第二个总体均值为1，标准差取自U(2, 5)，显然两个总体标准差不相等，那么在t检验时设定和不设定方差相等的选项对结果有多大影响？把两种情况的P值都画出来：左图是原始P值，可见基本在对角线上，说明大致相等，若眼神儿不好，可看右图，即P值的差异，可见方差不等时P值偏大（原因很简单，因为Welch校正的自由度小于等于不校正的自由度，样本量相等的时候统计量的分母即标准误一样，因此统计量完全一样，自由度越小，P值越大嘛），但大多少呢？其实也没大多少。

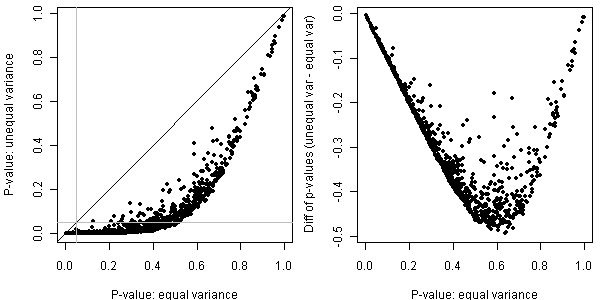
Welch/Satterthwaite当然不是吃饱了没事干，要校正自由度当然也是有用武之地的，尤其是当样本量严重不相等时，这两者的结果就差远了。把第一个样本量改成10，然后如法炮制：

par(mar = c(4, 4, 0.5, 0.5), mfrow = c(1, 2))
set.seed(123)
plot(pval <- t(replicate(1000, {
    x1 = rnorm(10, mean = 0, sd = runif(1, 0.5, 1))
    x2 = rnorm(100, mean = 1, sd = runif(1, 2, 5))
    c(t.test(x1, x2, var.equal = TRUE)$p.value, t.test(x1, x2,
        var.equal = FALSE)$p.value)
})), xlab = "P-value: equal variance", ylab = "P-value: unequal variance",
    pch = 20, asp = 1)
abline(0, 1)
abline(h = 0.05, v = 0.05, col = "gray")
plot(pval[, 1], pval[, 2] - pval[, 1], xlab = "P-value: equal variance",
    ylab = "Diff of p-values (unequal var - equal var)", pch = 20)

这文章，上COS主站寒酸了点，有人能扩展一下就好了。不过这个过程倒是可以提醒广大人民群众避免“路见不平一声吼，吼完继续往前走”，尤其是懒得翻公式的人（像我这样），遇见问题，可以偷懒用计算的方法找答案。

附“大家来找茬”一则：第二次的代码和第一次有啥不一样（除了样本量变了之外）？为啥有这么个变化？这小子想干啥？