小提琴图没什么特别的,就是把密度估计放在一根对称轴的两边,然后竖起来就可以了。我们可以把它看做箱线图的同伴;箱线图只是展示了分位数的位置,小提琴图展示了任意位置的密度,通过小提琴图我们可以知道哪些位置的密度较高。另外,我们也可以把多个小提琴放在一起比较。如下图:
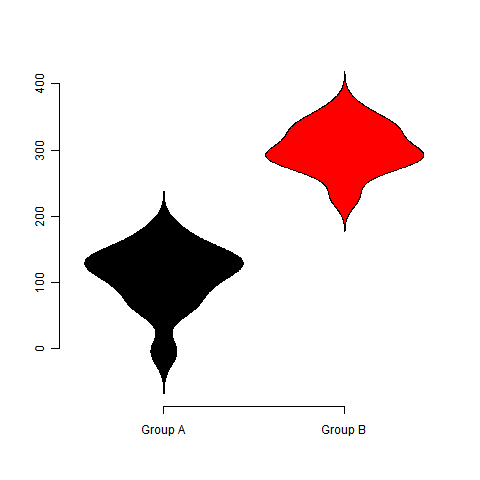
所用函数simple.violinplot()来自于UsingR包,不过它没有提供填充不同颜色的功能,上图是我修改了源代码之后作出来的。问题来自于Adelaide大学的Fernando Marmolejo Ramos,他在R-help里面问了没人回答,所以就给我私人Email了。
不多写了,不然到时候书卖不出去了。
library(UsingR)
violin.colors = function(x, ..., orientation = "vertical",
bw = "nrd0", names = NULL, from = NULL, to = from, pars = NULL,
col = NA) {
args <- list(x, ...)
namedargs <- if (!is.null(attributes(args)$names))
attributes(args)$names != ""
else rep(FALSE, length = length(args))
pars <- c(args[namedargs], pars)
groups <- if (is.list(x))
x
else args[!namedargs]
if (0 == (n <- length(groups)))
stop("invalid first argument")
if (length(class(groups)))
groups <- unclass(groups)
if (!missing(names))
attr(groups, "names") <- names
else {
if (is.null(attr(groups, "names")))
attr(groups, "names") <- 1:n
names <- attr(groups, "names")
}
xvals <- matrix(0, nr = 512, nc = n)
yvals <- matrix(0, nr = 512, nc = n)
center <- 1:n
for (i in 1:n) {
if (is.null(from))
tmp.dens <- density(groups[[i]], bw = bw)
else tmp.dens <- density(groups[[i]], bw = bw, from = from,
to = to)
xvals[, i] <- tmp.dens$x
yvals.needtoscale <- tmp.dens$y
yvals.scaled <- 7/16 * yvals.needtoscale/max(yvals.needtoscale)
yvals[, i] <- yvals.scaled
}
if (orientation == "vertical") {
xrange <- c(1/2, n + 1/2)
yrange <- range(xvals)
}
else {
xrange <- range(xvals)
yrange <- c(min(yvals), max(yvals))
}
plot.new()
plot.window(xlim = xrange, ylim = yrange)
for (i in 1:n) vlnplt(xvals[, i], yvals[, i], center[i],
bordercolor = rainbow(i), bgcolor = rainbow(n - i), orientation = orientation,
col = col[i], ...)
axis(1, at = 1:n, labels = names)
axis(2)
}
a = rnorm(25, 100, 50)
b = rnorm(25, 300, 50)
violin.colors(list("Group A" = a, "Group B" = b), col = 1:2)