I feel unhappy, so I just decide to write something not-so-interesting.
Everybody is using Structural Equation Models (SEM) in China as if it were shameful that you didn’t construct SEMs in your paper. Again, few people know SEM theories – not to say the computation issues. They don’t care, because they know this is a so-called advanced tool. This morning I’ve talked about several ironic things about SEM in my speech.
The theory can be regarded as easy, though in fact it’s not. The main idea is to develop a model with a theoretical covariance matrix ($\Sigma$) which is similar to the sample covariance matrix S. Therefore, how to minimize their discrepancy becomes the most critical part in parameter estimation. Common discrepancy functions can be derived through maximum likelihood (ML), unweighted least squares (ULS) and generalized least squares (GLS), etc. Take ML as an example, the discrepancy function is
$$FML = tr(S\Sigma-1) + \log|\Sigma| - log|S| - (p + q)$$
This function is quite complicated; usually it has more than 20 parameters. All along I have been doubting the reliability of its optimization (the dimension is really too high!). However, nobody ever mentioned this problem. Maybe they’re too happy to notice it.
OK, since my topic is the implementation in R, let’s check the package “sem” first. The function sem() is used to fit general structural equation models.
sem {sem} R Documentation
**General Structural Equation Models **
**Description**
`sem` fits general structural equation models (with both observed and unobserved variables) by the method of maximum likelihood, assuming multinormal errors. Observed variables are also called _indicators_ or _manifest variables_; unobserved variables are also called _factors_ or _latent variables_. Normally, the generic function (`sem`) would be used.
**Usage**
sem(ram, ...)
## S3 method for class 'mod':
sem(ram, S, N, obs.variables=rownames(S), fixed.x=NULL, debug=FALSE, ...)
## Default S3 method:
sem(ram, S, N, param.names = paste("Param", 1:t, sep = ""),
var.names = paste("V", 1:m, sep = ""), fixed.x = NULL, raw=FALSE,
debug = FALSE, analytic.gradient = TRUE, warn = FALSE, maxiter = 500,
par.size=c('ones', 'startvalues'), refit=TRUE, start.tol=1E-6, ...)
startvalues(S, ram, debug = FALSE, tol=1E-6)
## S3 method for class 'sem':
print(x, ...)
## S3 method for class 'sem':
summary(object, digits=5, conf.level=0.9, ...)
## S3 method for class 'sem':
deviance(object, ...)
## S3 method for class 'sem':
df.residual(object, ...)
Currently only ML and_ two-stage least squares (TSLS) _are available in this package. The specification is easy: just tell R your sample covariance matrix and settings for coefficients and covariances. The examples are quite clear:
# Note: These examples can't be run via example() because the default file
# argument of specify.model() requires that the model specification be entered
# at the command prompt. The examples can be copied and run in the R console,
# however. See ?specify.model for further information
## Not run:
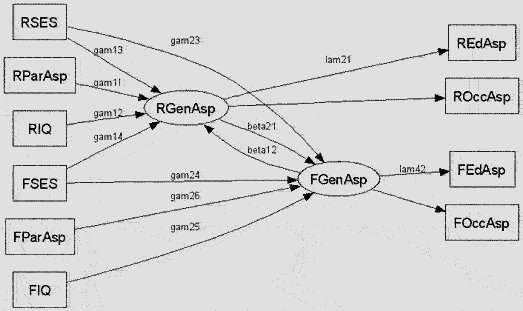
# ------------- Duncan, Haller and Portes peer-influences model ----------------------
# A nonrecursive SEM with unobserved endogenous variables and fixed exogenous variables
R.DHP <- matrix(c( # lower triangle of correlation matrix
1, 0, 0, 0, 0, 0, 0, 0, 0, 0,
.6247, 1, 0, 0, 0, 0, 0, 0, 0, 0,
.3269, .3669, 1, 0, 0, 0, 0, 0, 0, 0,
.4216, .3275, .6404, 1, 0, 0, 0, 0, 0, 0,
.2137, .2742, .1124, .0839, 1, 0, 0, 0, 0, 0,
.4105, .4043, .2903, .2598, .1839, 1, 0, 0, 0, 0,
.3240, .4047, .3054, .2786, .0489, .2220, 1, 0, 0, 0,
.2930, .2407, .4105, .3607, .0186, .1861, .2707, 1, 0, 0,
.2995, .2863, .5191, .5007, .0782, .3355, .2302, .2950, 1, 0,
.0760, .0702, .2784, .1988, .1147, .1021, .0931, -.0438, .2087, 1
), ncol=10, byrow=TRUE)
rownames(R.DHP) <- colnames(R.DHP) <-
c('ROccAsp', 'REdAsp', 'FOccAsp', 'FEdAsp', 'RParAsp', 'RIQ',
'RSES', 'FSES', 'FIQ', 'FParAsp')
# Fit the model using a symbolic ram specification
model.dhp <- specify.model()
RParAsp -> RGenAsp, gam11, NA
RIQ -> RGenAsp, gam12, NA
RSES -> RGenAsp, gam13, NA
FSES -> RGenAsp, gam14, NA
RSES -> FGenAsp, gam23, NA
FSES -> FGenAsp, gam24, NA
FIQ -> FGenAsp, gam25, NA
FParAsp -> FGenAsp, gam26, NA
FGenAsp -> RGenAsp, beta12, NA
RGenAsp -> FGenAsp, beta21, NA
RGenAsp -> ROccAsp, NA, 1
RGenAsp -> REdAsp, lam21, NA
FGenAsp -> FOccAsp, NA, 1
FGenAsp -> FEdAsp, lam42, NA
RGenAsp <-> RGenAsp, ps11, NA
FGenAsp <-> FGenAsp, ps22, NA
RGenAsp <-> FGenAsp, ps12, NA
ROccAsp <-> ROccAsp, theta1, NA
REdAsp <-> REdAsp, theta2, NA
FOccAsp <-> FOccAsp, theta3, NA
FEdAsp <-> FEdAsp, theta4, NA
sem.dhp.1 <- sem(model.dhp, R.DHP, 329,
fixed.x=c('RParAsp', 'RIQ', 'RSES', 'FSES', 'FIQ', 'FParAsp'))
summary(sem.dhp.1)
## Model Chisquare = 26.697 Df = 15 Pr(>Chisq) = 0.031302
## Chisquare (null model) = 872 Df = 45
## Goodness-of-fit index = 0.98439
## Adjusted goodness-of-fit index = 0.94275
## RMSEA index = 0.048759 90
## Bentler-Bonnett NFI = 0.96938
## Tucker-Lewis NNFI = 0.95757
## Bentler CFI = 0.98586
## BIC = -60.244
##
## Normalized Residuals
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## -0.7990 -0.1180 0.0000 -0.0120 0.0397 1.5700
##
## Parameter Estimates
## Estimate Std Error z value Pr(>|z|)
## gam11 0.161224 0.038487 4.1890 2.8019e-05 RGenAsp <--- RParAsp
## gam12 0.249653 0.044580 5.6001 2.1428e-08 RGenAsp <--- RIQ
## gam13 0.218404 0.043476 5.0235 5.0730e-07 RGenAsp <--- RSES
## gam14 0.071843 0.050335 1.4273 1.5350e-01 RGenAsp <--- FSES
## gam23 0.061894 0.051738 1.1963 2.3158e-01 FGenAsp <--- RSES
## gam24 0.228868 0.044495 5.1437 2.6938e-07 FGenAsp <--- FSES
## gam25 0.349039 0.044551 7.8346 4.6629e-15 FGenAsp <--- FIQ
## gam26 0.159535 0.040129 3.9755 7.0224e-05 FGenAsp <--- FParAsp
## beta12 0.184226 0.096207 1.9149 5.5506e-02 RGenAsp <--- FGenAsp
## beta21 0.235458 0.119742 1.9664 4.9255e-02 FGenAsp <--- RGenAsp
## lam21 1.062674 0.091967 11.5549 0.0000e+00 REdAsp <--- RGenAsp
## lam42 0.929727 0.071152 13.0668 0.0000e+00 FEdAsp <--- FGenAsp
## ps11 0.280987 0.046311 6.0674 1.2999e-09 RGenAsp <--> RGenAsp
## ps22 0.263836 0.044902 5.8759 4.2067e-09 FGenAsp <--> FGenAsp
## ps12 -0.022601 0.051649 -0.4376 6.6168e-01 FGenAsp <--> RGenAsp
## theta1 0.412145 0.052211 7.8939 2.8866e-15 ROccAsp <--> ROccAsp
## theta2 0.336148 0.053323 6.3040 2.9003e-10 REdAsp <--> REdAsp
## theta3 0.311194 0.046665 6.6687 2.5800e-11 FOccAsp <--> FOccAsp
## theta4 0.404604 0.046733 8.6578 0.0000e+00 FEdAsp <--> FEdAsp
##
## Iterations = 28
# Fit the model using a numerical ram specification
ram.dhp <- matrix(c(
# heads to from param start
1, 1, 11, 0, 1,
1, 2, 11, 1, NA, # lam21
1, 3, 12, 0, 1,
1, 4, 12, 2, NA, # lam42
1, 11, 5, 3, NA, # gam11
1, 11, 6, 4, NA, # gam12
1, 11, 7, 5, NA, # gam13
1, 11, 8, 6, NA, # gam14
1, 12, 7, 7, NA, # gam23
1, 12, 8, 8, NA, # gam24
1, 12, 9, 9, NA, # gam25
1, 12, 10, 10, NA, # gam26
1, 11, 12, 11, NA, # beta12
1, 12, 11, 12, NA, # beta21
2, 1, 1, 13, NA, # theta1
2, 2, 2, 14, NA, # theta2
2, 3, 3, 15, NA, # theta3
2, 4, 4, 16, NA, # theta4
2, 11, 11, 17, NA, # psi11
2, 12, 12, 18, NA, # psi22
2, 11, 12, 19, NA # psi12
), ncol=5, byrow=TRUE)
params.dhp <- c('lam21', 'lam42', 'gam11', 'gam12', 'gam13', 'gam14',
'gam23', 'gam24', 'gam25', 'gam26',
'beta12', 'beta21', 'theta1', 'theta2', 'theta3', 'theta4',
'psi11', 'psi22', 'psi12')
vars.dhp <- c('ROccAsp', 'REdAsp', 'FOccAsp', 'FEdAsp', 'RParAsp', 'RIQ',
'RSES', 'FSES', 'FIQ', 'FParAsp', 'RGenAsp', 'FGenAsp')
sem.dhp.2 <- sem(ram.dhp, R.DHP, 329, params.dhp, vars.dhp, fixed.x=5:10)
summary(sem.dhp.2)
## Model Chisquare = 26.697 Df = 15 Pr(>Chisq) = 0.031302
## Chisquare (null model) = 872 Df = 45
## Goodness-of-fit index = 0.98439
## Adjusted goodness-of-fit index = 0.94275
## RMSEA index = 0.048759 90
## Bentler-Bonnett NFI = 0.96938
## Tucker-Lewis NNFI = 0.95757
## Bentler CFI = 0.98586
## BIC = -60.244
##
## Normalized Residuals
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## -0.7990 -0.1180 0.0000 -0.0120 0.0397 1.5700
##
## Parameter Estimates
## Estimate Std Error z value Pr(>|z|)
## lam21 1.062674 0.091967 11.5549 0.0000e+00 REdAsp <--- RGenAsp
## lam42 0.929727 0.071152 13.0668 0.0000e+00 FEdAsp <--- FGenAsp
## gam11 0.161224 0.038487 4.1890 2.8019e-05 RGenAsp <--- RParAsp
## gam12 0.249653 0.044580 5.6001 2.1428e-08 RGenAsp <--- RIQ
## gam13 0.218404 0.043476 5.0235 5.0730e-07 RGenAsp <--- RSES
## gam14 0.071843 0.050335 1.4273 1.5350e-01 RGenAsp <--- FSES
## gam23 0.061894 0.051738 1.1963 2.3158e-01 FGenAsp <--- RSES
## gam24 0.228868 0.044495 5.1437 2.6938e-07 FGenAsp <--- FSES
## gam25 0.349039 0.044551 7.8346 4.6629e-15 FGenAsp <--- FIQ
## gam26 0.159535 0.040129 3.9755 7.0224e-05 FGenAsp <--- FParAsp
## beta12 0.184226 0.096207 1.9149 5.5506e-02 RGenAsp <--- FGenAsp
## beta21 0.235458 0.119742 1.9664 4.9255e-02 FGenAsp <--- RGenAsp
## theta1 0.412145 0.052211 7.8939 2.8866e-15 ROccAsp <--> ROccAsp
## theta2 0.336148 0.053323 6.3040 2.9003e-10 REdAsp <--> REdAsp
## theta3 0.311194 0.046665 6.6687 2.5800e-11 FOccAsp <--> FOccAsp
## theta4 0.404604 0.046733 8.6578 0.0000e+00 FEdAsp <--> FEdAsp
## psi11 0.280987 0.046311 6.0674 1.2999e-09 RGenAsp <--> RGenAsp
## psi22 0.263836 0.044902 5.8759 4.2067e-09 FGenAsp <--> FGenAsp
## psi12 -0.022601 0.051649 -0.4376 6.6168e-01 RGenAsp <--> FGenAsp
Iterations = 28
# -------------------- Wheaton et al. alienation data ----------------------
S.wh <- matrix(c(
11.834, 0, 0, 0, 0, 0,
6.947, 9.364, 0, 0, 0, 0,
6.819, 5.091, 12.532, 0, 0, 0,
4.783, 5.028, 7.495, 9.986, 0, 0,
-3.839, -3.889, -3.841, -3.625, 9.610, 0,
-21.899, -18.831, -21.748, -18.775, 35.522, 450.288),
6, 6)
rownames(S.wh) <- colnames(S.wh) <-
c('Anomia67','Powerless67','Anomia71','Powerless71','Education','SEI')
# This is the model in the SAS manual for PROC CALIS: A Recursive SEM with
# latent endogenous and exogenous variables.
# Curiously, both factor loadings for two of the latent variables are fixed.
model.wh.1 <- specify.model()
Alienation67 -> Anomia67, NA, 1
Alienation67 -> Powerless67, NA, 0.833
Alienation71 -> Anomia71, NA, 1
Alienation71 -> Powerless71, NA, 0.833
SES -> Education, NA, 1
SES -> SEI, lamb, NA
SES -> Alienation67, gam1, NA
Alienation67 -> Alienation71, beta, NA
SES -> Alienation71, gam2, NA
Anomia67 <-> Anomia67, the1, NA
Anomia71 <-> Anomia71, the1, NA
Powerless67 <-> Powerless67, the2, NA
Powerless71 <-> Powerless71, the2, NA
Education <-> Education, the3, NA
SEI <-> SEI, the4, NA
Anomia67 <-> Anomia71, the5, NA
Powerless67 <-> Powerless71, the5, NA
Alienation67 <-> Alienation67, psi1, NA
Alienation71 <-> Alienation71, psi2, NA
SES <-> SES, phi, NA
sem.wh.1 <- sem(model.wh.1, S.wh, 932)
summary(sem.wh.1)
## Model Chisquare = 13.485 Df = 9 Pr(>Chisq) = 0.14186
## Chisquare (null model) = 2131.4 Df = 15
## Goodness-of-fit index = 0.99527
## Adjusted goodness-of-fit index = 0.98896
## RMSEA index = 0.023136 90
## Bentler-Bonnett NFI = 0.99367
## Tucker-Lewis NNFI = 0.99647
## Bentler CFI = 0.99788
## BIC = -48.051
##
## Normalized Residuals
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## -1.26000 -0.13100 0.00014 -0.02870 0.11400 0.87400
##
## Parameter Estimates
## Estimate Std Error z value Pr(>|z|)
## lamb 5.36880 0.433982 12.3710 0.0000e+00 SEI <--- SES
## gam1 -0.62994 0.056128 -11.2233 0.0000e+00 Alienation67 <--- SES
## beta 0.59312 0.046820 12.6680 0.0000e+00 Alienation71 <--- Alienation67
## gam2 -0.24086 0.055202 -4.3632 1.2817e-05 Alienation71 <--- SES
## the1 3.60787 0.200589 17.9864 0.0000e+00 Anomia67 <--> Anomia67
## the2 3.59494 0.165234 21.7567 0.0000e+00 Powerless67 <--> Powerless67
## the3 2.99366 0.498972 5.9996 1.9774e-09 Education <--> Education
## the4 259.57583 18.321121 14.1681 0.0000e+00 SEI <--> SEI
## the5 0.90579 0.121710 7.4422 9.9032e-14 Anomia71 <--> Anomia67
## psi1 5.67050 0.422906 13.4084 0.0000e+00 Alienation67 <--> Alienation67
## psi2 4.51481 0.334993 13.4773 0.0000e+00 Alienation71 <--> Alienation71
## phi 6.61632 0.639506 10.3460 0.0000e+00 SES <--> SES
##
## Iterations = 78
# The same model, but treating one loading for each latent variable as free.
model.wh.2 <- specify.model()
Alienation67 -> Anomia67, NA, 1
Alienation67 -> Powerless67, lamby, NA
Alienation71 -> Anomia71, NA, 1
Alienation71 -> Powerless71, lamby, NA
SES -> Education, NA, 1
SES -> SEI, lambx, NA
SES -> Alienation67, gam1, NA
Alienation67 -> Alienation71, beta, NA
SES -> Alienation71, gam2, NA
Anomia67 <-> Anomia67, the1, NA
Anomia71 <-> Anomia71, the1, NA
Powerless67 <-> Powerless67, the2, NA
Powerless71 <-> Powerless71, the2, NA
Education <-> Education, the3, NA
SEI <-> SEI, the4, NA
Anomia67 <-> Anomia71, the5, NA
Powerless67 <-> Powerless71, the5, NA
Alienation67 <-> Alienation67, psi1, NA
Alienation71 <-> Alienation71, psi2, NA
SES <-> SES, phi, NA
sem.wh.2 <- sem(model.wh.2, S.wh, 932)
summary(sem.wh.2)
## Model Chisquare = 12.673 Df = 8 Pr(>Chisq) = 0.12360
## Chisquare (null model) = 2131.4 Df = 15
## Goodness-of-fit index = 0.99553
## Adjusted goodness-of-fit index = 0.98828
## RMSEA index = 0.025049 90
## Bentler-Bonnett NFI = 0.99405
## Tucker-Lewis NNFI = 0.99586
## Bentler CFI = 0.9978
## BIC = -42.026
##
## Normalized Residuals
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## -0.997000 -0.140000 0.000295 -0.028800 0.100000 0.759000
##
## Parameter Estimates
## Estimate Std Error z value Pr(>|z|)
## lamby 0.86261 0.033383 25.8402 0.0000e+00 Powerless67 <--- Alienation67
## lambx 5.35302 0.432591 12.3743 0.0000e+00 SEI <--- SES
## gam1 -0.62129 0.056142 -11.0663 0.0000e+00 Alienation67 <--- SES
## beta 0.59428 0.047040 12.6335 0.0000e+00 Alienation71 <--- Alienation67
## gam2 -0.23580 0.054684 -4.3121 1.6173e-05 Alienation71 <--- SES
## the1 3.74499 0.249823 14.9906 0.0000e+00 Anomia67 <--> Anomia67
## the2 3.49378 0.200754 17.4033 0.0000e+00 Powerless67 <--> Powerless67
## the3 2.97409 0.499661 5.9522 2.6456e-09 Education <--> Education
## the4 260.13252 18.298141 14.2163 0.0000e+00 SEI <--> SEI
## the5 0.90377 0.121818 7.4190 1.1791e-13 Anomia71 <--> Anomia67
## psi1 5.47380 0.464073 11.7951 0.0000e+00 Alienation67 <--> Alienation67
## psi2 4.36410 0.362722 12.0315 0.0000e+00 Alienation71 <--> Alienation71
## phi 6.63576 0.640425 10.3615 0.0000e+00 SES <--> SES
##
## Iterations = 79
##
# ----------------------- Thurstone data ---------------------------------------
# Second-order confirmatory factor analysis, from the SAS manual for PROC CALIS
R.thur <- matrix(c(
1., 0, 0, 0, 0, 0, 0, 0, 0,
.828, 1., 0, 0, 0, 0, 0, 0, 0,
.776, .779, 1., 0, 0, 0, 0, 0, 0,
.439, .493, .460, 1., 0, 0, 0, 0, 0,
.432, .464, .425, .674, 1., 0, 0, 0, 0,
.447, .489, .443, .590, .541, 1., 0, 0, 0,
.447, .432, .401, .381, .402, .288, 1., 0, 0,
.541, .537, .534, .350, .367, .320, .555, 1., 0,
.380, .358, .359, .424, .446, .325, .598, .452, 1.
), ncol=9, byrow=TRUE)
rownames(R.thur) <- colnames(R.Thur) <-
c('Sentences','Vocabulary','Sent.Completion','First.Letters',
'4.Letter.Words','Suffixes','Letter.Series','Pedigrees', 'Letter.Group')
model.thur <- specify.model()
F1 -> Sentences, lam11, NA
F1 -> Vocabulary, lam21, NA
F1 -> Sent.Completion, lam31, NA
F2 -> First.Letters, lam41, NA
F2 -> 4.Letter.Words, lam52, NA
F2 -> Suffixes, lam62, NA
F3 -> Letter.Series, lam73, NA
F3 -> Pedigrees, lam83, NA
F3 -> Letter.Group, lam93, NA
F4 -> F1, gam1, NA
F4 -> F2, gam2, NA
F4 -> F3, gam3, NA
Sentences <-> Sentences, th1, NA
Vocabulary <-> Vocabulary, th2, NA
Sent.Completion <-> Sent.Completion, th3, NA
First.Letters <-> First.Letters, th4, NA
4.Letter.Words <-> 4.Letter.Words, th5, NA
Suffixes <-> Suffixes, th6, NA
Letter.Series <-> Letter.Series, th7, NA
Pedigrees <-> Pedigrees, th8, NA
Letter.Group <-> Letter.Group, th9, NA
F1 <-> F1, NA, 1
F2 <-> F2, NA, 1
F3 <-> F3, NA, 1
F4 <-> F4, NA, 1
sem.thur <- sem(model.thur, R.thur, 213)
summary(sem.thur)
## Model Chisquare = 38.196 Df = 24 Pr(>Chisq) = 0.033101
## Chisquare (null model) = 1101.9 Df = 36
## Goodness-of-fit index = 0.95957
## Adjusted goodness-of-fit index = 0.9242
## RMSEA index = 0.052822 90
## Bentler-Bonnett NFI = 0.96534
## Tucker-Lewis NNFI = 0.98002
## Bentler CFI = 0.98668
## BIC = -90.475
##
## Normalized Residuals
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## -9.72e-01 -4.16e-01 -4.20e-07 4.01e-02 9.39e-02 1.63e+00
##
## Parameter Estimates
## Estimate Std Error z value Pr(>|z|)
## lam11 0.51512 0.064964 7.9293 2.2204e-15 Sentences <--- F1
## lam21 0.52031 0.065162 7.9849 1.3323e-15 Vocabulary <--- F1
## lam31 0.48743 0.062422 7.8087 5.7732e-15 Sent.Completion <--- F1
## lam41 0.52112 0.063137 8.2538 2.2204e-16 First.Letters <--- F2
## lam52 0.49707 0.059673 8.3298 0.0000e+00 4.Letter.Words <--- F2
## lam62 0.43806 0.056479 7.7562 8.6597e-15 Suffixes <--- F2
## lam73 0.45244 0.071371 6.3392 2.3100e-10 Letter.Series <--- F3
## lam83 0.41729 0.061037 6.8367 8.1020e-12 Pedigrees <--- F3
## lam93 0.40763 0.064524 6.3175 2.6584e-10 Letter.Group <--- F3
## gam1 1.44381 0.264173 5.4654 4.6184e-08 F1 <--- F4
## gam2 1.25383 0.216597 5.7888 7.0907e-09 F2 <--- F4
## gam3 1.40655 0.279331 5.0354 4.7681e-07 F3 <--- F4
## th1 0.18150 0.028400 6.3907 1.6517e-10 Sentences <--> Sentences
## th2 0.16493 0.027797 5.9334 2.9678e-09 Vocabulary <--> Vocabulary
## th3 0.26713 0.033468 7.9816 1.5543e-15 Sent.Completion <--> Sent.Completion
## th4 0.30150 0.050686 5.9484 2.7073e-09 First.Letters <--> First.Letters
## th5 0.36450 0.052358 6.9617 3.3618e-12 4.Letter.Words <--> 4.Letter.Words
## th6 0.50642 0.059963 8.4455 0.0000e+00 Suffixes <--> Suffixes
## th7 0.39033 0.061599 6.3367 2.3474e-10 Letter.Series <--> Letter.Series
## th8 0.48137 0.065388 7.3618 1.8141e-13 Pedigrees <--> Pedigrees
## th9 0.50510 0.065227 7.7437 9.5479e-15 Letter.Group <--> Letter.Group
##
## Iterations = 54
##
#------------------------- Kerchoff/Kenney path analysis ---------------------
# An observed-variable recursive SEM from the LISREL manual
R.kerch <- matrix(c(
1, 0, 0, 0, 0, 0, 0,
-.100, 1, 0, 0, 0, 0, 0,
.277, -.152, 1, 0, 0, 0, 0,
.250, -.108, .611, 1, 0, 0, 0,
.572, -.105, .294, .248, 1, 0, 0,
.489, -.213, .446, .410, .597, 1, 0,
.335, -.153, .303, .331, .478, .651, 1),
ncol=7, byrow=TRUE)
rownames(R.kerch) <- colnames(R.kerch) <- c('Intelligence','Siblings',
'FatherEd','FatherOcc','Grades','EducExp','OccupAsp')
model.kerch <- specify.model()
Intelligence -> Grades, gam51, NA
Siblings -> Grades, gam52, NA
FatherEd -> Grades, gam53, NA
FatherOcc -> Grades, gam54, NA
Intelligence -> EducExp, gam61, NA
Siblings -> EducExp, gam62, NA
FatherEd -> EducExp, gam63, NA
FatherOcc -> EducExp, gam64, NA
Grades -> EducExp, beta65, NA
Intelligence -> OccupAsp, gam71, NA
Siblings -> OccupAsp, gam72, NA
FatherEd -> OccupAsp, gam73, NA
FatherOcc -> OccupAsp, gam74, NA
Grades -> OccupAsp, beta75, NA
EducExp -> OccupAsp, beta76, NA
Grades <-> Grades, psi5, NA
EducExp <-> EducExp, psi6, NA
OccupAsp <-> OccupAsp, psi7, NA
sem.kerch <- sem(model.kerch, R.kerch, 737, fixed.x=c('Intelligence','Siblings',
'FatherEd','FatherOcc'))
summary(sem.kerch)
## Model Chisquare = 3.2685e-13 Df = 0 Pr(>Chisq) = NA
## Chisquare (null model) = 1664.3 Df = 21
## Goodness-of-fit index = 1
## BIC = 3.2685e-13
##
## Normalized Residuals
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## -4.28e-15 0.00e+00 0.00e+00 7.62e-16 1.47e-15 5.17e-15
##
## Parameter Estimates
## Estimate Std Error z value Pr(>|z|)
## gam51 0.525902 0.031182 16.86530 0.0000e+00 Grades <--- Intelligence
## gam52 -0.029942 0.030149 -0.99314 3.2064e-01 Grades <--- Siblings
## gam53 0.118966 0.038259 3.10951 1.8740e-03 Grades <--- FatherEd
## gam54 0.040603 0.037785 1.07456 2.8257e-01 Grades <--- FatherOcc
## gam61 0.160270 0.032710 4.89979 9.5940e-07 EducExp <--- Intelligence
## gam62 -0.111779 0.026876 -4.15899 3.1966e-05 EducExp <--- Siblings
## gam63 0.172719 0.034306 5.03461 4.7882e-07 EducExp <--- FatherEd
## gam64 0.151852 0.033688 4.50758 6.5571e-06 EducExp <--- FatherOcc
## beta65 0.405150 0.032838 12.33799 0.0000e+00 EducExp <--- Grades
## gam71 -0.039405 0.034500 -1.14215 2.5339e-01 OccupAsp <--- Intelligence
## gam72 -0.018825 0.028222 -0.66700 5.0477e-01 OccupAsp <--- Siblings
## gam73 -0.041333 0.036216 -1.14126 2.5376e-01 OccupAsp <--- FatherEd
## gam74 0.099577 0.035446 2.80924 4.9658e-03 OccupAsp <--- FatherOcc
## beta75 0.157912 0.037443 4.21738 2.4716e-05 OccupAsp <--- Grades
## beta76 0.549593 0.038260 14.36486 0.0000e+00 OccupAsp <--- EducExp
## psi5 0.650995 0.033946 19.17743 0.0000e+00 Grades <--> Grades
## psi6 0.516652 0.026943 19.17590 0.0000e+00 EducExp <--> EducExp
## psi7 0.556617 0.029026 19.17644 0.0000e+00 OccupAsp <--> OccupAsp
##
## Iterations = 0
#------------------- McArdle/Epstein latent-growth-curve model -----------------
# This model, from McArdle and Epstein (1987, p.118), illustrates the use of a
# raw moment matrix to fit a model with an intercept. (The example was suggested
# by Mike Stoolmiller.)
M.McArdle <- scan()
365.661 0 0 0 0
503.175 719.905 0 0 0
675.656 958.479 1303.392 0 0
890.680 1265.846 1712.475 2278.257 0
18.034 25.819 35.255 46.593 1.000
M.McArdle <- matrix(M.McArdle, 5, 5, byrow=TRUE)
rownames(M.McArdle) <- colnames(M.McArdle) <- scan(what="")
WISC1 WISC2 WISC3 WISC4 UNIT
mod.McArdle <- specify.model()
C -> WISC1, NA, 6.07
C -> WISC2, B2, NA
C -> WISC3, B3, NA
C -> WISC4, B4, NA
UNIT -> C, Mc, NA
C <-> C, Vc, NA,
WISC1 <-> WISC1, Vd, NA
WISC2 <-> WISC2, Vd, NA
WISC3 <-> WISC3, Vd, NA
WISC4 <-> WISC4, Vd, NA
sem.McArdle <- sem(mod.McArdle, M.McArdle, 204, fixed.x="UNIT", raw=TRUE)
summary(sem.McArdle)
## Model fit to raw moment matrix.
##
## Model Chisquare = 83.791 Df = 8 Pr(>Chisq) = 8.4377e-15
## BIC = 41.246
##
## Normalized Residuals
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## -0.15300 -0.01840 0.00132 -0.00576 0.02400 0.07760
##
## Parameter Estimates
## Estimate Std Error z value Pr(>|z|)
## B2 8.61354 0.135438 63.5976 0 WISC2 <--- C
## B3 11.64054 0.168854 68.9387 0 WISC3 <--- C
## B4 15.40323 0.213071 72.2916 0 WISC4 <--- C
## Mc 3.01763 0.060690 49.7219 0 C <--- UNIT
## Vc 0.44343 0.047704 9.2955 0 C <--> C
## Vd 11.78832 0.674060 17.4885 0 WISC1 <--> WISC1
##
## Iterations = 37
## End(Not run)
Besides, you may draw your path diagram (see the function path.diagram()) via the graph-drawing program dot; see Koutsofios and North (2002) and http://www.graphviz.org/ (also free & open-source). Below is a diagram I draw in dot:

In the end, I believe the function _boot.sem() _is worth our attention. As the model is too complicated, it’s natural to doubt its stability, so _bootstrapping _surely will be a good choice, which might be more reliable than the coefficients’ standard errors directly computed under the assumption of multi-normality. Bear in mind that bootstrapping takes some time, so be patient.