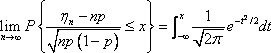这是SEM伟大工程第二步中的序曲(注意只是序曲)——大数定律和中心极限定理,目的是研究统计计算算法,尤其是Monte Carlo方法,因为据我所知,这玩意儿是基于大数定律的。学习至今,发现自己的基础是千疮百孔,惨不忍睹,遂把这些漏洞趁现在尽力补上。还有另外一个原因是看着别人动不动就叫唤:“俺的结论是有大数定律支持的!”然后就把听众吓坏了,因为有好些人自己也搞不清楚这所谓的Law of Large Numbers是个啥东东,于是,大家一起忽悠吧!
不是我贬损谁,确实有这样的例子。像王星老师上课讲有些学生,“我都这么大样本量了还不服从正态分布啊?”言下之意就是说只要搞到的数字足够多,那么就可以请出正态分布老祖宗了。这不扯的么?……我坦言,我自己对于大数定律和中心极限定理其实也是有些晕晕乎乎,还是有些怕所谓的测度论这些东西的,不过无论如何,我还是努力把这俩玩意儿清理明白吧。
首先看看究竟啥叫大数定律和中心极限定理。(下面的东西叫“定义”,不叫“证明”,当年某人为此还和我争了半天,真是想不明白这有什么好争的)
定义1 若ξ1, ξ2, …, ξn, …是随机变量序列,令
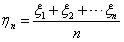
若存在常数序列a1, a2, …, an, …对任何的正数ε,恒有
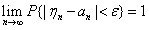
则称序列{ξn}服从大数定律(或大数法则)
定义2 对于独立随机变量序列ξ1, ξ2, …, ξn, …假定Eξn和Dξn都存在,令
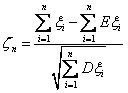
若
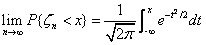
则称序列{ξn}服从中心极限定理(Central Limit Theorem)。
(1)切比雪夫(Chebyishev)不等式 它是切比雪夫大数定律的基础:
设随机变量X有数学期望E(X)与方差D(X),则对任意的正数ε,有
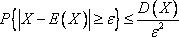
(2)大数定律
切比雪夫定理的特殊情况 设随机变量X1, X2, …, Xn相互独立,且具有相同的数学期望和方差:
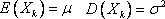
则对任意的正数ε,有
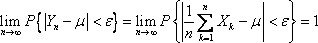
·贝努利定理 设nA是n次独立重复试验中事件A发生的次数,p是事件A在每次试验中发生的概率,则对任意的正数ε,有
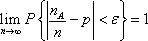
·辛钦定理 设X1, X2, …, Xn相互独立,服从同一分布,具有数学期望E(Xk)=μ,则对任意正数,有
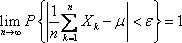
(3)中心极限定律
·同分布的中心极限定理 设X1, X2, …, Xn相互独立,服从同一分布,具有数学期望和方差:
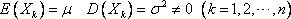
则对任意的x,恒有
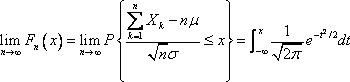
德莫佛-拉普拉斯定理 设随机变量ηn(n=1, 2, …)服从参数为n, p (0<p<1)的二项分布,