这是伟大的SEM工程之——Wishart分布篇!要用最大似然估计(ML)的话,目前似乎只有这一条路可走,今日强忍着看多元统计分析的书没吐出来,实在是佩服张尧庭老师,他简直不是人——只能说是神1……其中用到的高等代数证明我几乎一个都没看懂,汗如雨下。此分布由Wishart于1928年推导出来(因此我认为Wishart也不是人),据称有人就用这个时间作为多元统计分析的诞生时间,由此可见Wishart分布之牛X。废话少说,言归正传:
首先定义一个矩阵Xnxm=(xij)的分布,X的分布即其列向量一个个拼接起来形成的长向量的分布;若X是n阶对称矩阵,那么只需要取上三角(或下三角)部分组成长向量即可,此时
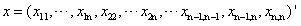
样本矩阵仍然是:

其中假定y(i)相互独立,且y(i)~Nm(μi, V),Y的期望记作:
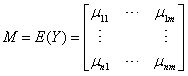
此时就可以给出Wishart分布的定义了。以下二式中,(1)式是非中心Wishart分布(τ≠0),(2)式是中心Wishart分布(τ=0):
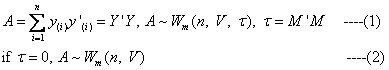
现隆重推出中心Wishart分布的密度函数:
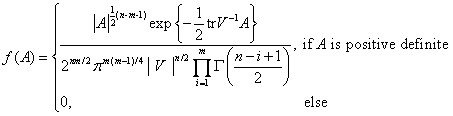
注意当A不是正定阵时,f(A)=0,在SEM参数的最大似然估计中,似乎没看见对A的正定性的检验,这是目前我的一点小疑问。现在给出密度函数之后,可以顺便说说SEM参数最大似然估计的思路:首先将结构方程模型中的样本标准化(如果只是做ML那么事实上只需要中心化就可以了),使各个样品的均值为零,这一步其实就是为中心Wishart分布做准备(使得τ=0),那么现在容易证明A其实就是样本协方差阵S。而SEM参数估计的关键工作(或者说目的)也就在于使理论推导出的协方差阵(Σ(θ))与实际样本协方差阵S尽可能接近;理论协方差阵Σ(θ)也就是上式密度函数中的V,那么现在要做的就是知道了S来估计Σ(θ),也即知道了A来估计V,正好就顺路上了最大似然估计的“贼船”,如果最大似然估计的原理忘了请参见尾注2。还有一点需要提醒注意的是,最大似然估计本身并没有直接达到使Σ(θ)与S尽量接近的目的,看估计的效果如何,还得在估计之后再对结果进行检验(拟合指数)。
-
我可以放话:世界上不容怀疑的事情只有两件——一是太阳从东边升起;二是张尧庭老师是神。 ↩︎
-
最大似然估计法(Maximum Likelihood Estimation):设
$X_1$,$X_2$, …,$X_n$是来自总体$X \sim f(x; \theta)$(其中$\theta$未知)的样本,而$x_1$,$x_2$, …,$x_n$为样本值,使似然函数$$L(\theta;x_1,x_2,\ldots,x_n)=f(x_1;\theta) f(x_2;\theta) \cdots f(x_n;\theta)$$达到最大的
$\hat{\theta}$称为参数$\theta$的最大似然估计值。一般地,$\theta$的最大似然估计值$\hat{\theta}$满足:$$\frac{d \ln L}{d \theta}=0$$↩︎