Write An R Package Using Literate Programming Techniques

This is an example of writing an R package using the Literate Programming (LP) technique, implemented through the knitr package and Makefile. It only shows you the idea, and I do not mean you must use knitr, R Markdown, or Makefile. The full source code of this rlp package is available on Github. To build this package, you need to install R packages knitr and rmarkdown. Windows users also need to install Rtools, which includes the utility make. Linux and macOS users should have make ready by default.

Literate Programming

Interestingly, the most popular application of the LP paradigm seems to be documenting software (using a special form of comments) for users instead of “programming” for authors. In other words, we use LP to document the usage of software, instead of documenting the source code. See Doxygen, Javadoc, and roxygen2 for examples. There exists one exception, though, in the LaTeX world¹. Some LaTeX package authors write both LaTeX code and documentation in a single document, and weave it into a PDF document that contains both the source code and documentation. I’m not a LaTeX expert, and it is probably well-known that I have big headache when looking at a full screen of backslashes, from \documentclass{}, \begin{document}, \alpha, \beta, \texttt{}, …, and all the way to \end{document}.

I do not find LP for LaTeX appealing, but that does not mean LP itself is not an appealing idea. On the contrary, I believe it can be very interesting and useful when it is applied to your own favorite language, e.g., R for me. In my opinion, LP has at least two advantages:

1. You can write much more extensive and richer documentation than you normally could do with comments. In general, comments in code are (or should be) brief and limited to plain text. Normally you will not write five paragraphs of comments to explain a few lines of code, and you cannot write readable² math expressions or embed a video in comments.
2. You can label code chunks and reference/reuse them using the labels, which allows you to compose your program flexibly using different pieces of code chunks. For example, you can define and explain a code chunk later in the document, but insert it in a previous code chunk using its label. This feature has been emphasized by Knuth, but I do not see it is widely adopted for some reason. Perhaps most people are more comfortable with designing a big program by smaller units like functions instead of code chunks, which is actually a good idea.

Personally I find the first advantage more convincing, although it seems some LP folks just love the second one. For R package development, I guess it will be inconvenient for unit testing if we use the LP idea instead of writing smaller functions, because testing functions is straightforward, but testing code chunks is not. Anyway, I will show both features of LP mentioned above in this document.

Setup

First, I set a few knitr chunk options:

knitr::opts_chunk$set(eval = FALSE, tidy = FALSE)

I set eval = FALSE because this document mostly serves as the documentation of our R source code, and I do not really need to run the code chunks here. The code will be generated to the R/ directory, then built by R CMD build into an R package. If you do want to execute a code chunk, you can use the chunk option eval = TRUE on that code chunk. Another important reason that you may not want to evaluate some code chunks is that they may not be complete, for example, when you insert documentation in the middle of a function to explain a few lines of the function body.

In this document, you will see the chunk option purl = FALSE occasionally, and that means I want to exclude these code chunks when extracting the R code, but I do want to include them when compiling this document to HTML.

R Code Chunks

Now I write some example R code chunks using the R Markdown syntax. Here I define a boring function add_one() with an argument x, and it simply does x + 1:

#' A cool function
#' 
#' Well, not really cool. Just add 1 to x.
#' @param x a numeric vector
#' @export
#' @examples
#' add_one(1)
#' add_one(1:10)
add_one = function(x) {
  x + 1
}

Besides the R source code, I also wrote the R documentation using the roxygen2 syntax. This R code chunk will be extracted and placed under the R/ directory later. The critical step is how to extract the code chunk. After this step, you will be in a familiar world of roxygen2::roxygenize(), or devtools::build(), or R CMD build, or whatever package building process you like.

From Rmd to R

I put this Rmd file under the vignettes/ directory, and you do not have to use this directory. I’m using it because I will get a nice by-product after R CMD build, which is the package vignette. I used rmarkdown to generate an HTML vignette, which is visually pleasant to read in my eyes.

To extract the code chunks from the Rmd documents, I used a Makefile under the root directory of this package³:

purl=Rscript -e "knitr::purl('$(1)', '$(2)', quiet=TRUE, documentation=0)"

rfiles:=$(patsubst vignettes/LP-%.Rmd,R/%-GEN.R,$(wildcard vignettes/LP-*.Rmd))

all: $(rfiles)

R/%-GEN.R: vignettes/LP-%.Rmd
	$(call purl,$^,$@)

I defined a function purl in the Makefile, which calls the R function knitr::purl() to extract code chunks from Rmd to R. To make sure I do not purl arbitrary Rmd documents, I added a prefix LP- to the Rmd filenames, and only these files will be processed. Similarly, to make sure make does not use arbitrary R files as targets, I added a suffix -GEN (stands for “generated”) to the R filenames. To put it short, an Rmd file vignettes/LP-foo.Rmd will generate R/foo-GEN.R. The variable rfiles stores all the potential R scripts to be generated. If you are familiar with make, you will immediately see its advantage here: foo-GEN.R will be re-generated only if LP-foo.Rmd has been updated.

You may have realized that this leads to two copies of R code: one copy in Rmd, and one in R. Therefore you need to remind your collaborators (if you have any) that they must not edit the R code under R/ that is generated from Rmd, but should edit the Rmd source documents instead.⁴

One Button to Rule Them All

Now we have three things to do to fully build this package:

1. Run make to generate R source code to R/;
2. Run roxygen2 to generate R documentation to man/, NAMESPACE, and other stuff;
3. Run R CMD build to build the package as well as the vignettes.

You certainly do not want to type these commands repeatedly. Unfortunately, due to the fact that this is not the standard process of building an R package, there is not a natural solution to combine the three steps into one. For power users, this is certainly not true – you can always write a shell script to do everything. But some users just do not know how to open a terminal to type commands, and you should not blame them – not all people do programming for a living, and a command window is not the only or ultimate solution of all problems.

So let’s start hacking and find a button to click. I have been secretly hacking the Build & Reload button in my RStudio IDE for a long time. If you open this rlp package in RStudio, and go to Tools -> Project Options -> Build Tools, you will see a weird configuration:

-v && Rscript -e "Rd2roxygen::rab(install=T,before=system('make'))"

At this moment, I’m not going to explain what it means since it is just a dirty hack, and please do not ask me, either. Let’s wait for the RStudio IDE to give us more freedom to customize the package build options in the future. If you are interested in the idea of LP for R packages, just copy my configuration, but bear in mind that it may stop working at some point. I will update this document when that happens.

Note Rd2roxygen::rab() is my own way of building R packages, and you certainly do not have to follow it. For example, if you are more comfortable with devtools, you can do⁵:

-v && make -C rlp && Rscript -e "devtools::install('rlp')"

Call Functions in This Package

You can certainly load the package and call the functions in this document, because the package vignettes are compiled after the package is temporarily installed⁶. For example, I call add_one() defined above:

library(rlp)
add_one(1)

## [1] 2

add_one(1:10)

##  [1]  2  3  4  5  6  7  8  9 10 11

Running live examples and generating output like this may help you explain what your functions actually do, so readers can understand your source code better, otherwise they can only reason about the code in their mind.

A Less Naive Example

Life is certainly not always as simple as add_one(). In this section, I give a slightly more advanced example to show how LP can be useful and relevant to developing R packages. Let’s consider the maximum likelihood estimation (MLE) for the parameters of the Gamma distribution \(\Gamma(y; \alpha, \beta)\).

I will use the function optim() to optimize the log-likelihood function. First, I define an R function with arguments data and start:

#' MLE for the Gamma distribution
#' 
#' Estimate the parameters (alpha and beta) of the Gamma distribution
#' using maximum likelihood.
#' @param data the data vector assumed to be generated from the Gamma 
#'   distribution
#' @param start the initial values for the parameters of the Gamma
#' distribution (passed to \code{\link{optim}()})
#' @param vcov whether to return an approximate variance-covariance
#' matrix of the parameter vector
#' @return A list with elements \code{estimate} (parameter estimates
#'   for alpha and beta) and, if \code{vcov = TRUE}, \code{vcov} (the
#'   variance-covariance matrix of the parameter vector).
#' @export
mle_gamma = function(data, start = c(1, 1), vcov = FALSE) {

The Gamma distribution has two commonly used parameterizations (shape-rate or shape-scale), and I will use the following probability density function (shape-rate):

$$f(x|\alpha,\beta)=\frac{\beta^{\alpha}}{\Gamma(\alpha)}x^{\alpha-1}\exp(-\beta x);\quad x>0$$

The log-density function is:

$$\log f=\alpha\log\beta-\log\Gamma(\alpha)+(\alpha-1)\log x-\beta x$$

The log-likelihood function given the data vector \(\mathbf{x}=[x_1,x_2,\ldots,x_n]\) will be:

$$L(\alpha,\beta|\mathbf{x})=n(\alpha\log(\beta)-\log(\Gamma(\alpha)))+(\alpha-1)\sum_{i=1}^{n}\log(x_{i})-\beta\sum_{i=1}^{n}x_{i}$$

And I define it in R as loglike(), where param is the parameter vector \([\alpha, \beta]\), and x is the data vector:

  loglike = function(param, x) {
    a = param[1]  # alpha (the shape parameter)
    b = param[2]  # beta (the rate parameter)
    n = length(x)
    n * (a * log(b) - lgamma(a)) + (a - 1) * sum(log(x)) - b * sum(x)
  }

It is worth noting that in practice we will rarely translate the math equation to R code like that for the Gamma distribution, since R has the dgamma() function that is much more efficient than the raw log-density function I used above. You would use sum(dgamma(x, shape = param[1], rate = param[2], log = TRUE)) instead. Anyway, I took the silly way just for demonstrating the LP idea instead of how to write efficient statistical computing code.

Next I optimize the log-likelihood function by passing the initial guesses and the data vector to it:

  opt = optim(start, loglike, x = data, hessian = vcov, control = list(fnscale = -1))

You need to be cautious that optim() minimizes the objective function by default, and that is why I used control = list(fnscale = -1). Then I’m minimizing -loglike, and essentially maximizing loglike. I need to make sure the optimization has reached convergence:

  if (opt$convergence != 0) stop('optim() failed to converge')
  res = list(estimate = opt$par)

Finally, I give an estimate of the variance-covariance matrix \(Var([\hat{\alpha},\hat{\beta}]')\) if vcov = TRUE:

  if (vcov) res$vcov = solve(-opt$hessian)

The estimate is the inverse of the negative Hessian matrix, because \(Var(\hat{\theta})=I^{-1}(\theta)\) for the maximum likelihood estimator \(\hat{\theta}\), where \(I(\theta)\) is the Information matrix, and we know \(I(\theta) = -E(H(\theta))\). In theory, \(I(\theta)\) is unknown, and I just use the observed information matrix, i.e., the negative Hessian matrix returned from optim(). Note the inverse matrix is computed via solve().

  res
}

The object res is returned, and we can use it to compute the confidence intervals of the parameters since MLE is asymptotically Normal. Now let’s try the function:

set.seed(1228)
d = rgamma(100, shape = 5, rate = 2)  # simulate some data from Gamma(5, 2)
r = mle_gamma(d, vcov = TRUE)
str(r)

## List of 2
##  $ estimate: num [1:2] 5.3 2.06
##  $ vcov    : num [1:2, 1:2] 0.529 0.206 0.206 0.088

The estimates are not too bad, compared to their true values. I can also give a 95% confidence interval for the parameter \(\alpha\), of which the estimate is asymptotically Normal:

a = r$estimate[1]  # estimate of alpha
s = sqrt(r$vcov[1, 1])  # standard error of the estimate of alpha
z = qnorm(1 - 0.05/2)  # 97.5% Normal quantile
c(a - z * s, a + z * s)  # a 95% CI

## [1] 3.876 6.727

Below is a histogram of the simulated data, with the true density curve, the true mean (solid vertical line), and the estimated mean (dashed line):⁷

par(mar = c(4, 4, .2, .1))
hist(d, main = '', col = 'darkgray', border = 'white', freq = FALSE)
curve(dgamma(x, shape = 5, rate = 2), 0, 6, add = TRUE, lwd = 2)
abline(v = c(5/2, r$estimate[1]/r$estimate[2]), lty = c(1, 2))

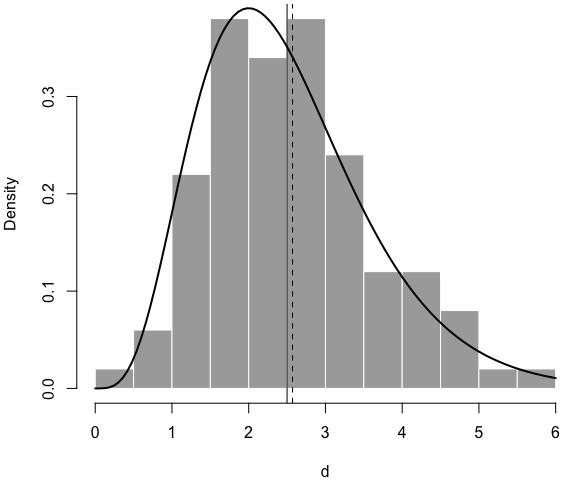
Now you see I can thoroughly explain an R function using LP. I’m not saying this is what you should do for all R functions, but sometimes there are cases in which you want something beyond code comments, such as math equations and graphics.

Apparently LP is more for those who want to understand your source code (including your future self!) than for end-users of your package. For most users, they probably just want to read the help page of the function, in which case they just type the question mark in R, e.g., ?mle_gamma.

Chunk References

I mentioned before that we could label code chunks and reference them to compose a bigger code chunk. Now I show a simple example of simulating from a bivariate Normal distribution. A bit background:

$$\left[\begin{array}{c} X\\ Y \end{array}\right]\sim\mathcal{N}\left(\left[\begin{array}{c} \mu_{X}\\ \mu_{Y} \end{array}\right],\left[\begin{array}{cc} \sigma_{X}^{2} & \rho\sigma_{X}\sigma_{Y}\\ \rho\sigma_{X}\sigma_{Y} & \sigma_{Y}^{2} \end{array}\right]\right)$$

One way to simulate from the bivariate Normal distribution is to first simulate from the marginal distribution \(f(x)\), then simulate from \(f(y|x)\). Below is the final simulation function:

#' Sample from a bivariate Normal distribution
#' 
#' Simulate x from the marginal f(x), then y from f(y|x), and
#' the pair (x, y) has the desired joint distribution.
#' @param n the desired sample size
#' @param m1,m2 the means of X and Y, respectively
#' @param s1,s2 the standard deviations of X and Y, respectively
#' @param rho the correlation coefficient between X and Y
#' @return A numeric matrix of two columns X and Y.
#' @export
rbinormal = function(n, m1 = 0, m2 = 0, s1 = 1, s2 = 1, rho = 0) {
  # warning: this is not an efficient implementation; you should use
  # vectorization in practice
  res = replicate(n, {
    x = rnorm(1, m1, s1)  # simulate from the marginal f(x)
    m2cond = m2 + s2/s1 * rho * (x - m1)  # conditional mean of Y
    s2cond = sqrt(1 - rho^2) * s2  # conditional sd of Y
    y = rnorm(1, m2cond, s2cond)  # simulate from the conditional f(y|x)
    c(x, y)
  })
  res = t(res)  # transpose the 2xn matrix to nx2
  colnames(res) = c('X', 'Y')
  res
}

If you are reading the source R Markdown document, you will see <<simulate_x>> and <<simulate_y>> instead of the real R code. The token <<>> denotes the code chunks defined below with the chunk labels simulate_x and simulate_y, respectively:

x = rnorm(1, m1, s1)  # simulate from the marginal f(x)

The marginal distribution of \(X\) is \(\mathcal{N}(\mu_X, \sigma^2_X)\), and we know the conditional distribution of \(Y|X\) is:

$$Y|X=x \sim \mathcal{N}\left(\mu_{Y}+\frac{\sigma_{Y}}{\sigma_{X}}\rho(x-\mu_{X}),\,(1-\rho^{2})\sigma_{Y}^{2}\right)$$

m2cond = m2 + s2/s1 * rho * (x - m1)  # conditional mean of Y
s2cond = sqrt(1 - rho^2) * s2  # conditional sd of Y
y = rnorm(1, m2cond, s2cond)  # simulate from the conditional f(y|x)

I just reused these code chunks in the function body of rbinormal(), instead of cutting and pasting the code there. As usual, I can test my function by examples:

set.seed(1229)
z = rbinormal(500, m1 = -1, s1 = 5, m2 = 3, s2 = .5, rho = -.7)
par(mar = c(4, 4, .2, .1))
plot(z, pch = 20, col = 'darkgray')
# the center of the bivariate dist
points(-1, 3, pch = 19, col = 'red', cex = 3)

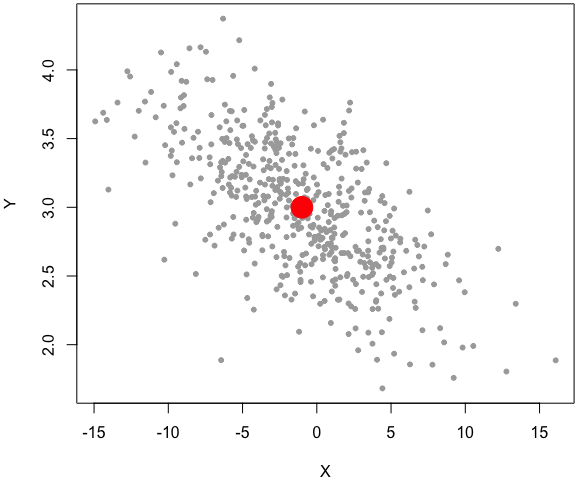
In this example, I factored out the code from the main function as two separate code chunks, and explained each later, instead of inserting the explanations in the middle of the function body. Again, the simulation code in this example is computationally inefficient, and it is only for demo purposes⁸.

Conclusions

This document has demonstrated that LP can be useful for package authors to explain their code in fine detail, which may not be easy to achieve by only using comments in code. Not everyone needs or wants to understand your source code, but clear explanations of your code will benefit both your future self, and more importantly, attract potential collaborators and contributors, hence increase the bus factor of your software packages, in this era of “social coding”.